- 완전 이진 트리의 일종
- 우선순위 큐를 위해 만들어진 자료구조
- 느슨한 정렬 상태 유지
- 큰 값이 상위 레벨에 있는 동시에 하위 레벨에도 존재 가능
- 부모 노드의 키 값이 자식 노드의 키 값보다 항상 작거나 큰 이진 트리
- 힙 트리에서는 중복된 값 허용

힙의 종류
- 최대 힙
- 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
- 최소 힙
- 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
힙 구현


- 자료구조 배열 사용(표준)
- 0번 인덱스 사용 x
- 부모 노드 자식 노드 관계
- 왼쪽 자식 노드 = (부모 인덱스) *2
- 오른쪽 자식 노드 = (부모 인덱스) *2 +1
- 부모 노드 = (자식 인덱스)/2
활용
- 시뮬레이션 시스템
- 네트워크 트래픽 제어
- 운영 체제에서의 작업 스케쥴링
- 수치 해석적인 계산

힙 연산자
- 삽입

// 최대 힙 삽입
void insert_heap(int input) {
Heap[++heapSize] = input; // 힙 크기를 하나 증가하고, 마지막 노드에 값 삽입
for( int i = heapSize; i > 1; i /= 2) {
// 마지막 노드가 자신의 부모 노드보다 크면 swap
if(Heap[i/2] < Heap[i]) {
swap(i/2, i);
} else {
break;
}
}
}- 삭제
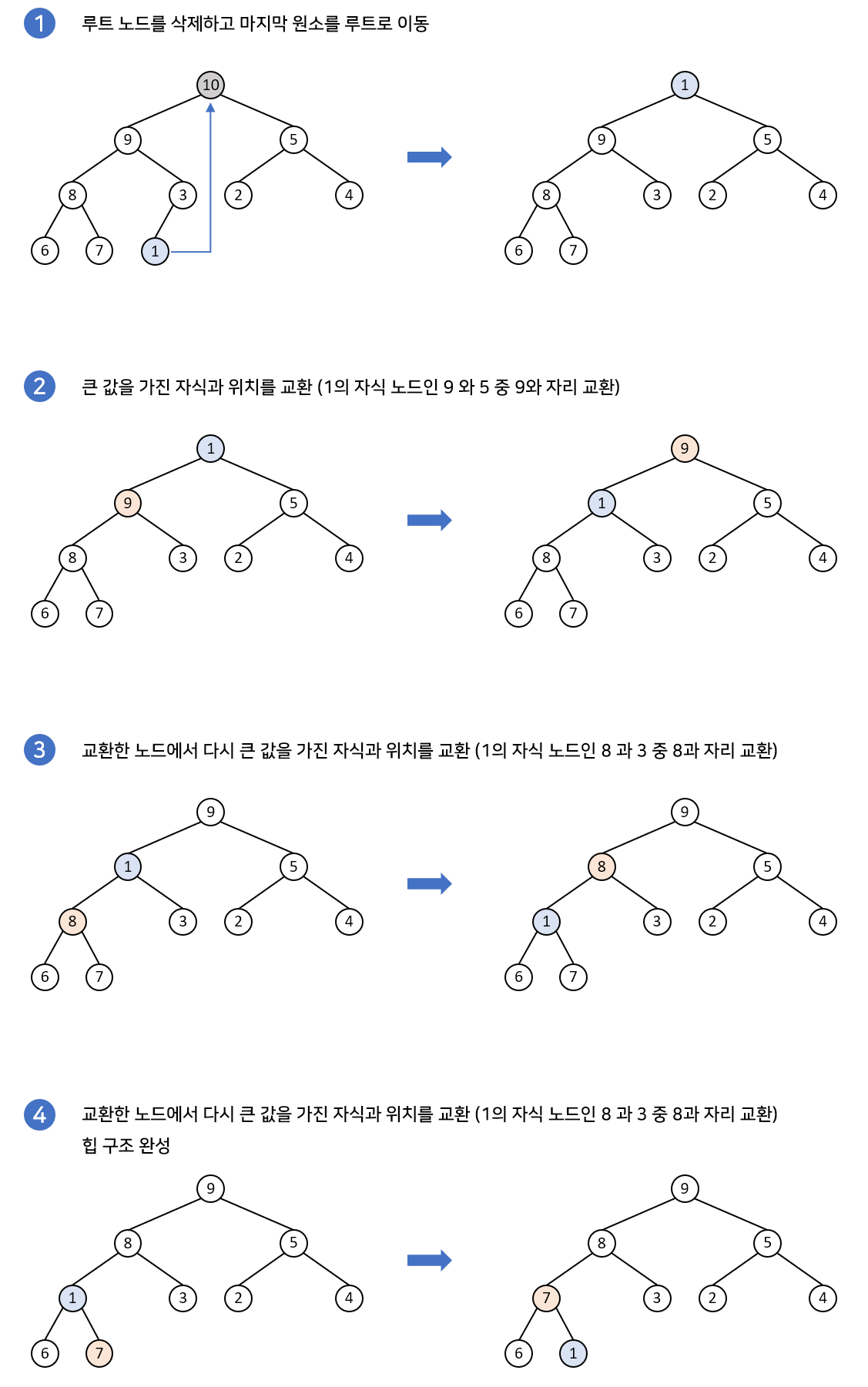
// 최대 힙 삭제
int delete_heap() {
if(heapSize == 0) // 배열이 비어있으면 리턴
return 0;
int result = Heap[1]; // 루트 노드의 값을 저장
Heap[1] = Heap[heapSize]; // 마지막 노드 값을 루트로 이동
Heap[heapSize--] = 0; // 마지막 노드 값을 초기화 후 사이즈 1 감소
for(int i = 1; i*2 <= heapSize;) {
// 마지막 노드 자식 노드들 보다 큰 경우
if(Heap[i] > Heap[i*2] && Heap[i] > Heap[i*2+1]) {
break;
}
// 왼쪽 자식 노드가 더 큰 경우
else if (Heap[i*2] > Heap[i*2+1]) {
swap(i, i*2);
i = i*2;
}
// 오른쪽 자식 노드가 더 큰 경우
else {
swap(i, i*2+1);
i = i*2+1;
}
}
return result;
}
이미지 출처 : https://velog.io/@emplam27/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B7%B8%EB%A6%BC%EC%9C%BC%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EB%8A%94-%ED%9E%99Heap
)
(이미지 출처 : https://velog.io/@emplam27/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B7%B8%EB%A6%BC%EC%9C%BC%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EB%8A%94-%ED%9E%99Heap
)
'자료구조' 카테고리의 다른 글
| [JAVA] Priority Queue (0) | 2023.07.06 |
|---|---|
| 덱(deque) (0) | 2023.02.02 |
| 큐 (0) | 2023.02.02 |
| 스택 (0) | 2023.02.02 |
